Abstract
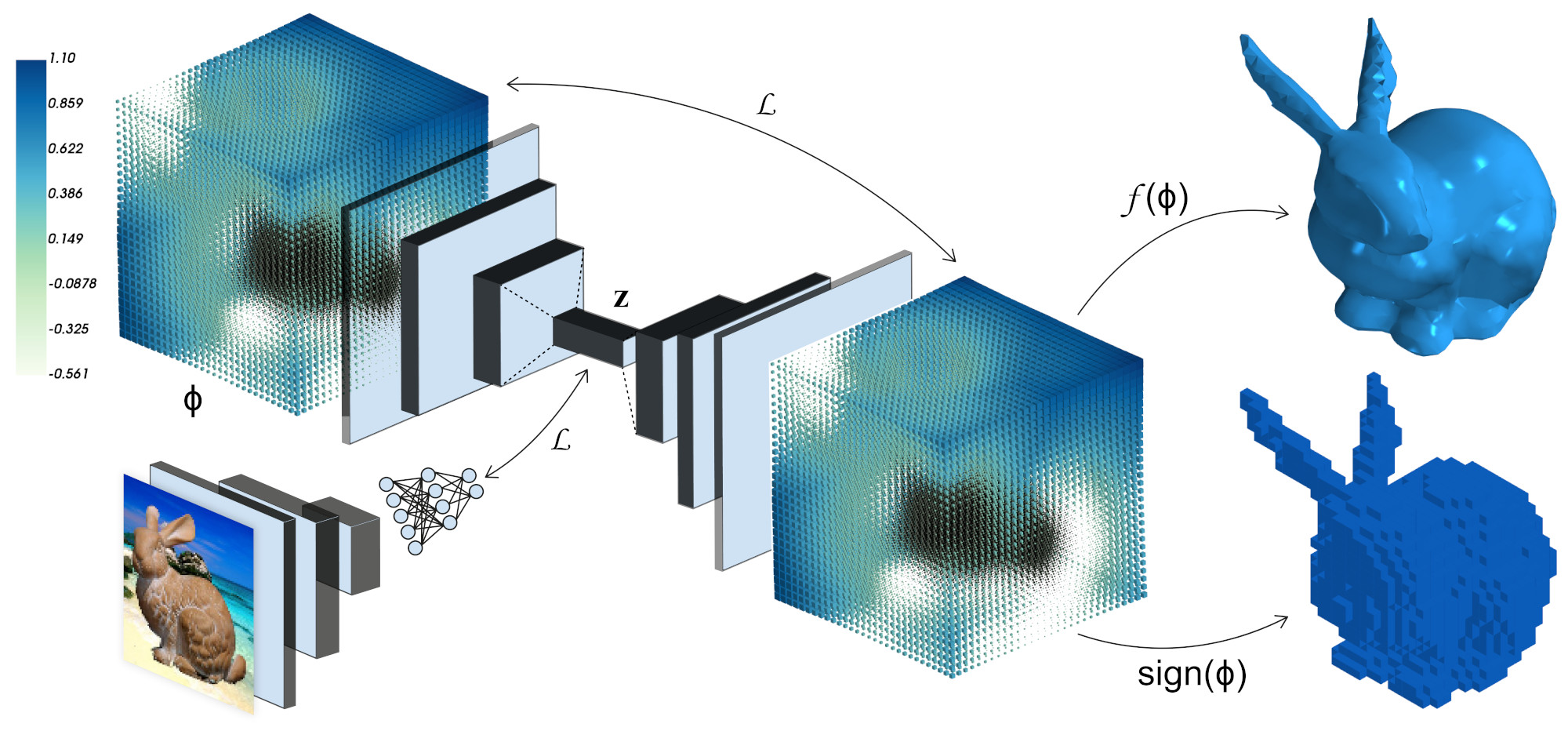
Implicit shape representations, such as Level Sets, provide a very elegant formulation for performing computations involving curves and surfaces. However, including implicit representations into canonical Neural Network formulations is far from straightforward. This has consequently restricted existing approaches to shape inference, to significantly less effective representations, perhaps most commonly voxels occupancy maps or sparse point clouds. To overcome this limitation we propose a novel formulation that permits the use of implicit representations of curves and surfaces, of arbitrary topology, as individual layers in Neural Network architectures with end-to-end trainability. Specifically, we propose to represent the output as an oriented level set of a continuous and discretised embedding function. We investigate the benefits of our approach on the task of 3D shape prediction from a single image and demonstrate its ability to produce a more accurate reconstruction compared to voxel-based representations. We further show that our model is flexible and can be applied to a variety of shape inference problems.
Results

