Abstract
We address the generalization ability of recent learning- based point cloud registration methods. Despite their success, these approaches tend to have poor performance when applied to mismatched conditions that are not well- represented in the training set, such as unseen object cat- egories, different complex scenes, or unknown depth sen- sors. In these circumstances, it has often been better to rely on classical non-learning methods (e.g., Iterative Clos- est Point), which have better generalization ability. Hybrid learning methods, that use learning for predicting point correspondences and then a deterministic step for alignment, have offered some respite, but are still limited in their generalization abilities. We revisit a recent innovation—PointNetLK—and show that the inclusion of an analytical Jacobian can exhibit remarkable generalization properties while reaping the inherent fidelity benefits of a learning framework. Our approach not only outperforms the state- of-the-art in mismatched conditions but also produces re- sults competitive with current learning methods when oper- ating on real-world test data close to the training set.
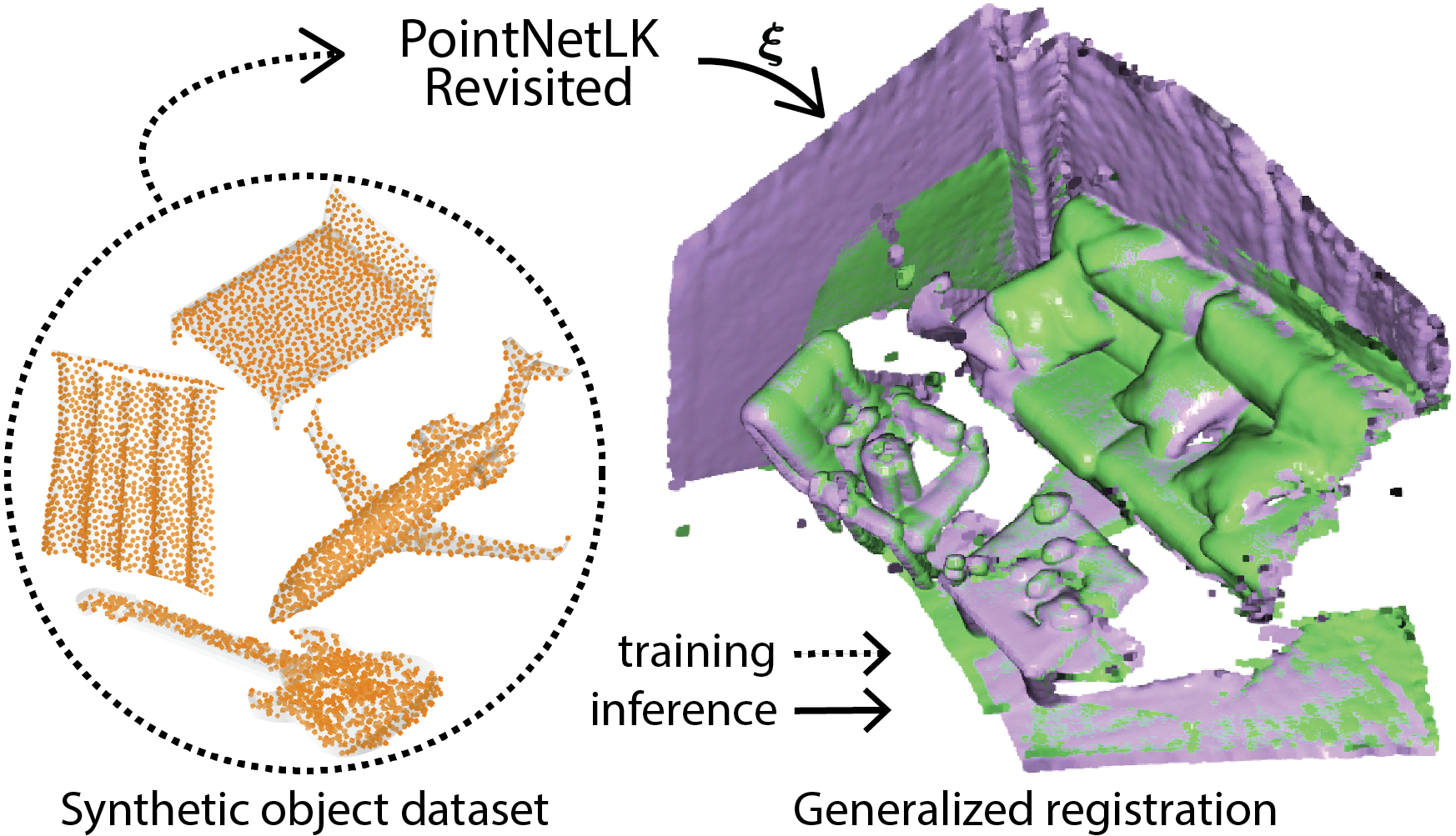Our analytical derivation of PointNetLK can be trained on a clean, dense, synthetic 3D object dataset and still accurately align noisy, sparse, real-world 3D scenes. Green is the template point cloud, purple is the registered point cloud, and the orange point clouds are an object training set. ξ are the rigid transformation parameters inferred by our method.
Visual results on complex, real-world scenes. Our voxelized analytical PointNetLK is able to register complex, real-world scenes with high fidelity. These scenes are from 8 different testing categories of the 3DMatch dataset. Purple is the registered scene and green is the template.
Video presentation
